-
Volumes 96-107 (2025)
-
Volume 106
-
Volume 105
-
Volume 104
-
Volume 103
Pages 1-314 (August 2025)
-
Volume 102
Pages 1-276 (July 2025)
-
Volume 101
Pages 1-166 (June 2025)
-
Volume 100
Pages 1-256 (May 2025)
-
Volume 99
Pages 1-242 (April 2025)
-
Volume 98
Pages 1-288 (March 2025)
-
Volume 97
Pages 1-256 (February 2025)
-
Volume 96
Pages 1-340 (January 2025)
-
Volume 106
-
Volumes 84-95 (2024)
-
Volume 95
Pages 1-392 (December 2024)
-
Volume 94
Pages 1-400 (November 2024)
-
Volume 93
Pages 1-376 (October 2024)
-
Volume 92
Pages 1-316 (September 2024)
-
Volume 91
Pages 1-378 (August 2024)
-
Volume 90
Pages 1-580 (July 2024)
-
Volume 89
Pages 1-278 (June 2024)
-
Volume 88
Pages 1-350 (May 2024)
-
Volume 87
Pages 1-338 (April 2024)
-
Volume 86
Pages 1-312 (March 2024)
-
Volume 85
Pages 1-334 (February 2024)
-
Volume 84
Pages 1-308 (January 2024)
-
Volume 95
-
Volumes 72-83 (2023)
-
Volume 83
Pages 1-258 (December 2023)
-
Volume 82
Pages 1-204 (November 2023)
-
Volume 81
Pages 1-188 (October 2023)
-
Volume 80
Pages 1-202 (September 2023)
-
Volume 79
Pages 1-172 (August 2023)
-
Volume 78
Pages 1-146 (July 2023)
-
Volume 77
Pages 1-152 (June 2023)
-
Volume 76
Pages 1-176 (May 2023)
-
Volume 75
Pages 1-228 (April 2023)
-
Volume 74
Pages 1-200 (March 2023)
-
Volume 73
Pages 1-138 (February 2023)
-
Volume 72
Pages 1-144 (January 2023)
-
Volume 83
-
Volumes 60-71 (2022)
-
Volume 71
Pages 1-108 (December 2022)
-
Volume 70
Pages 1-106 (November 2022)
-
Volume 69
Pages 1-122 (October 2022)
-
Volume 68
Pages 1-124 (September 2022)
-
Volume 67
Pages 1-102 (August 2022)
-
Volume 66
Pages 1-112 (July 2022)
-
Volume 65
Pages 1-138 (June 2022)
-
Volume 64
Pages 1-186 (May 2022)
-
Volume 63
Pages 1-124 (April 2022)
-
Volume 62
Pages 1-104 (March 2022)
-
Volume 61
Pages 1-120 (February 2022)
-
Volume 60
Pages 1-124 (January 2022)
-
Volume 71
- Volumes 54-59 (2021)
- Volumes 48-53 (2020)
- Volumes 42-47 (2019)
- Volumes 36-41 (2018)
- Volumes 30-35 (2017)
- Volumes 24-29 (2016)
- Volumes 18-23 (2015)
- Volumes 12-17 (2014)
- Volume 11 (2013)
- Volume 10 (2012)
- Volume 9 (2011)
- Volume 8 (2010)
- Volume 7 (2009)
- Volume 6 (2008)
- Volume 5 (2007)
- Volume 4 (2006)
- Volume 3 (2005)
- Volume 2 (2004)
- Volume 1 (2003)
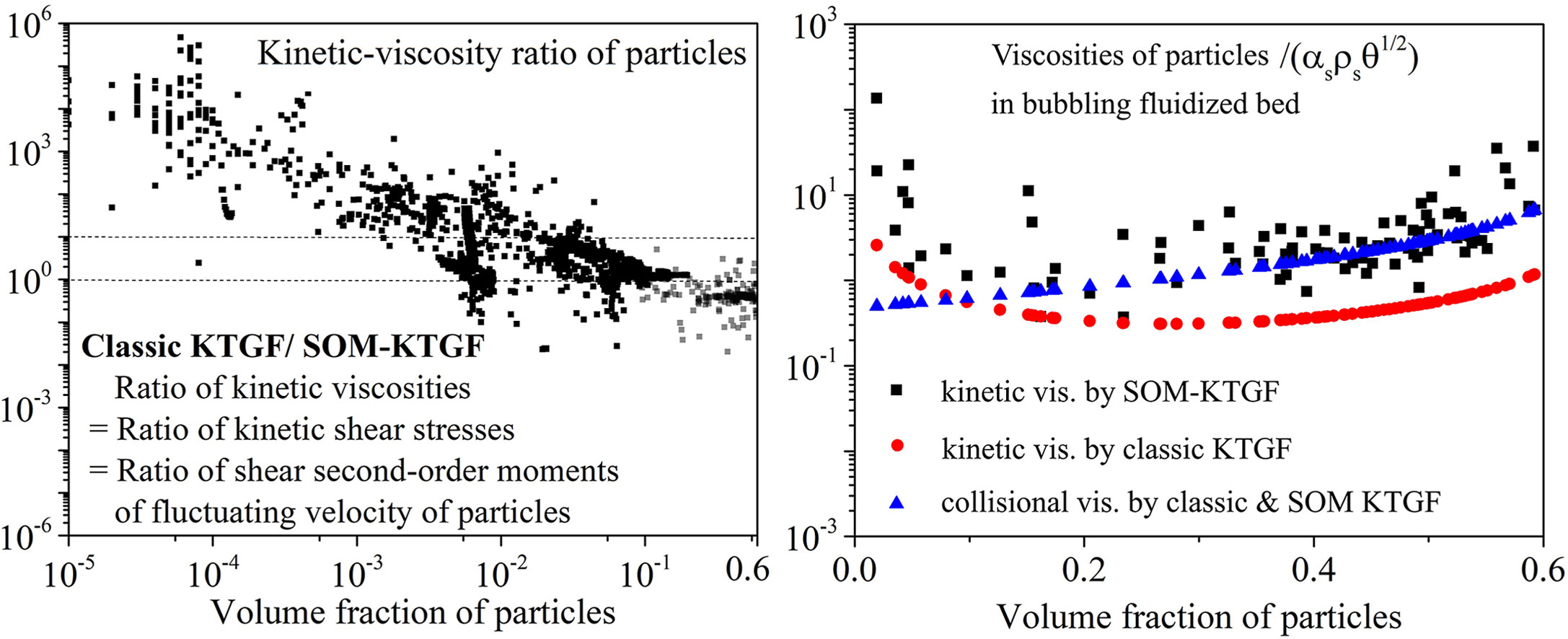
• Classic KTGF and SOM-KTGF differ in prediction of kinetic stress tensor.
• Compared kinetic shear stresses modelled by classic KTGF and SOM-KTGF.
• Kinetic viscosity over-predicted by classic KTGF in dilute phase of fluidization.
• Classic KTGF is equivalent to SOM-KTGF in dense phase particles of fluidization.
• SOM-KTGF is superior to classic KTGF in dense phase particles of fluidization.
Kinetic viscosity of particles in the kinetic theory of granular flow (KTGF) was derived from the turbulence viscosity of the gas phase based on the kinetic theory of gas, with the effects of the dense phase of granular materials. KTGF is prominent in predicting the dense particle flow, being the primary numerical method for the gas-particle flow in fluidization, predominantly in the large-scale simulations as a Eulerian method. Recent studies presented that the second-order moment (SOM) of KTGF is superior to the classic KTGF in the particle-flow prediction. The difference between classic KTGF and SOM KTGF exists in the numerical model of the kinetic stresses of particles, which is calculated by the pseudo kinetic viscosity of particles in classic KTGF and by the SOM of the fluctuating velocity of particles by using the partial differential equations in SOM-KTGF. In this study, the gas-particle flow was simulated using SOM-KTGF and the stress tensors of particles predicted by the two methods were compared. It was demonstrated that the normal components of the kinetic stress tensor predicted by the two methods were close in value. However, the kinetic shear-stress was over-predicted by the classic KTGF in the dilute phase of particles in the gas-particle flow of fluidization, when the volume fraction of particles was less than 0.01. Therefore, SOM-KTGF is superior to the classic KTGF, particularly when the particle flow is dominated by the interstitial gas phase, as the particle-laden flow occurs in the lower volume fraction of particles in the dense regime, and further in the dilute and median regimes, when the volume fraction of particles less than 0.01. This superiority is caused by the high-fidelity prediction of the kinetic shear stress in SOM-KTGF rather than the prediction by classic KTGF. In addition, SOM-KTGF extended the application of KTGF from dense flows of particles in fluidization to median-dilute flows of particles in pneumatic conveying, when the volume fraction is less than 0.001.