An operational variable of cement vertical roller mill modeling: Forecast process control variables by neural network RBF-MLP-GMDH--颗粒学报PARTICUOLOGY

Fatahi, R., Abdollahi, H., Noaparast, M., & Hadizadeh, M. (2025). An operational variable of cement vertical roller mill modeling: Forecast process control variables by neural network RBF-MLP-GMDH. Particuology, 103, 55-66. https://doi.org/10.1016/j.partic.2025.05.007

An operational variable of cement vertical roller mill modeling: Forecast process control variables by neural network RBF-MLP-GMDH

Rasoul Fatahi, Hadi Abdollahi^*, Mohammad Noaparast, Mehdi Hadizadeh

School of Mining Engineering, College of Engineering, University of Tehran, Tehran, Iran

10.1016/j.partic.2025.05.007

Volume 103, August 2025, Pages 55-66

Received 8 August 2024, Revised 25 January 2025, Accepted 5 May 2025, Available online 17 May 2025, Version of Record 29 May 2025.

E-mail: h_abdollahi@ut.ac.ir

Highlights

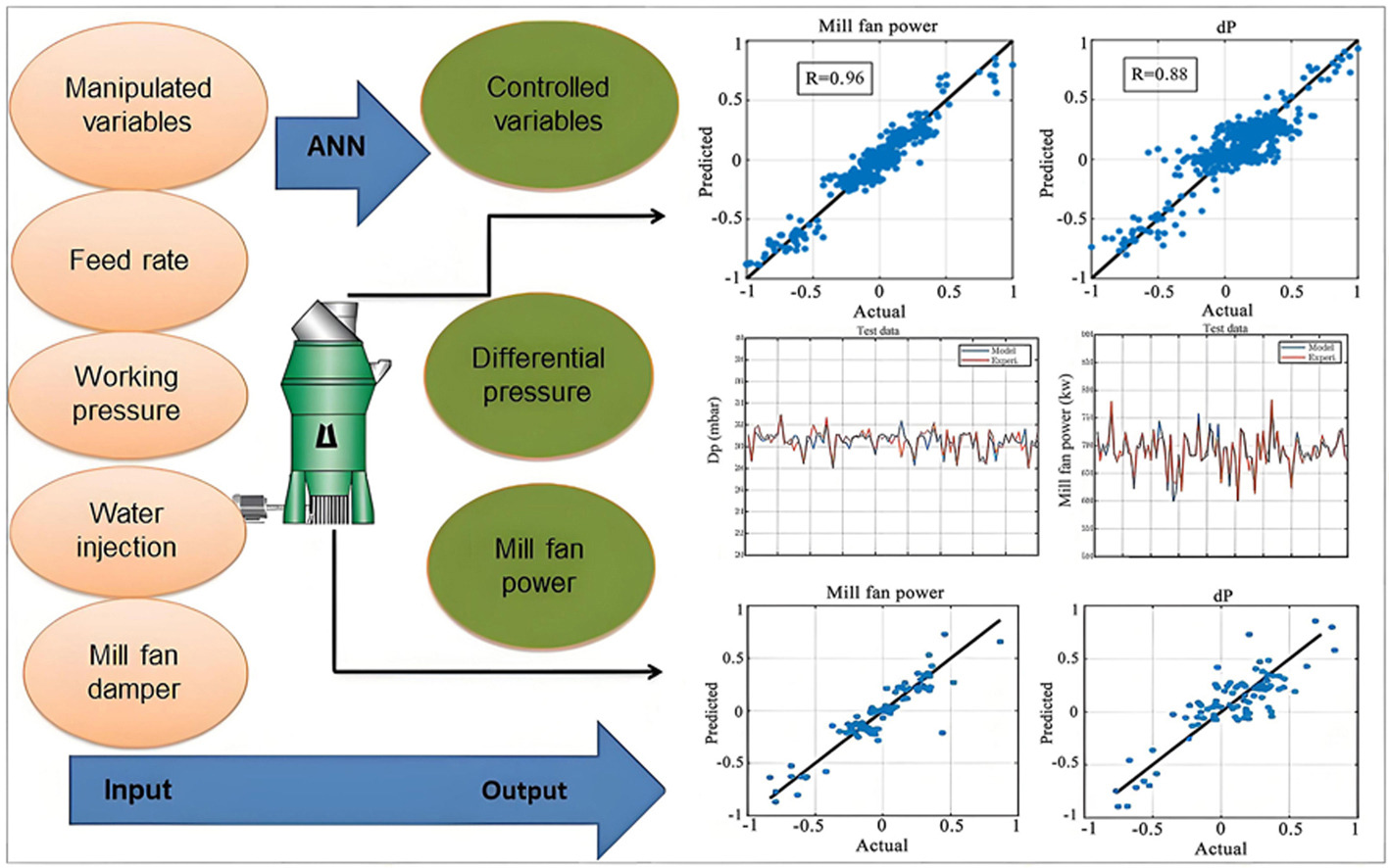
• MLP model results provided a more robust prediction than RBF and GMDH.

• MLP showed the highest accuracy and could predict the mill fan power and differential pressure.

• MLP revealed that feed rate, pressure, water injection, and fan dampers affect ventilation.

• Input-output relationships provided a more detailed insight into mill ventilation.

• Modeling revealed material transportation depends on differential pressure and mill fan power.

Abstract

Vertical Roller Mills)VRM (are highly favored in cement due to low power consumption, increased capacity, and process simplification. The VRM's grinding process involves a variety of operating parameters, including process-controlled and process-manipulated variables. Therefore, understanding interactions between operation variables and power consumption would be essential for sustainable ground material transportation during the ventilation process in the mill. A few investigations were conducted to model the ventilation and power consumption of VRMs. Using an Artificial Neural Network)ANN) model on large-scale industry problems could help understand how VRM variables interact and encourage controlling ventilation for long-term operations and altered production. The deficiencies were resolved by developing the ANN models such as Multi Layer Perceptron (MLP), Radial Basis Function (RBF), and Group Method of Data Handling (GMDH) for modeling differential pressure and mill fan power draw of a VRM grinding circuit to address the effectiveness of operating variables. The MLP model had the highest level of prediction accuracy for modeling, with a coefficient of predictive accuracy (R-value) of 0.96. The MLP assessment indicated that the most influential controlled variables were the feed rate, working pressure, water injection, and mill fan damper on the differential pressure and mill fan power. These results are consistent with the actual operating state of the VRM grinding circuit. Such an ANN model for a VRM can train operators, control the process, save time and energy, reduce laboratory work and scale issues, and enhance the operation's sustainability.

Graphical abstract

Keywords

ANN; Modeling; VRM; Ventilation; Mill power draw

文章导读