Data driven analysis of particulate systems for development of reliable model to determine drag coefficient of non-spherical particles--颗粒学报PARTICUOLOGY

Hussain, T., Ullah, A., Khalid, R. Z., Ahmad, F., Li, F., & Khan, A. (2025). Data driven analysis of particulate systems for development of reliable model to determine drag coefficient of non-spherical particles. Particuology, 97, 219-235. https://doi.org/10.1016/j.partic.2024.12.006

Data driven analysis of particulate systems for development of reliable model to determine drag coefficient of non-spherical particles

Tauseeq Hussain^a, Atta Ullah^a *, Rehan Zubair Khalid^{a b}, Farooq Ahmad^c, Fei Li^d, Asifullah Khan^{b e}

a Department of Chemical Engineering, Pakistan Institute of Engineering and Applied Sciences, Islamabad, 45650, Pakistan
b PIEAS Artificial Intelligence Center, Pakistan Institute of Engineering and Applied Sciences, Nilore, Islamabad, 45650, Pakistan
c Department of Chemical and Materials Engineering, College of Engineering, Northern Border University, Arar, Saudi Arabia
d Institute of Process Engineering, Chinese Academy of Sciences, Beijing, China
e Pattern Recognition Lab, Department of Computer and Information Sciences, Pakistan Institute of Engineering and Applied Sciences, Nilore, Islamabad, 45650, Pakistan

10.1016/j.partic.2024.12.006

Volume 97, February 2025, Pages 219-235

Received 17 September 2024, Revised 25 November 2024, Accepted 17 December 2024, Available online 3 January 2025, Version of Record 17 January 2025.

E-mail: atta@pieas.edu.pk

Highlights

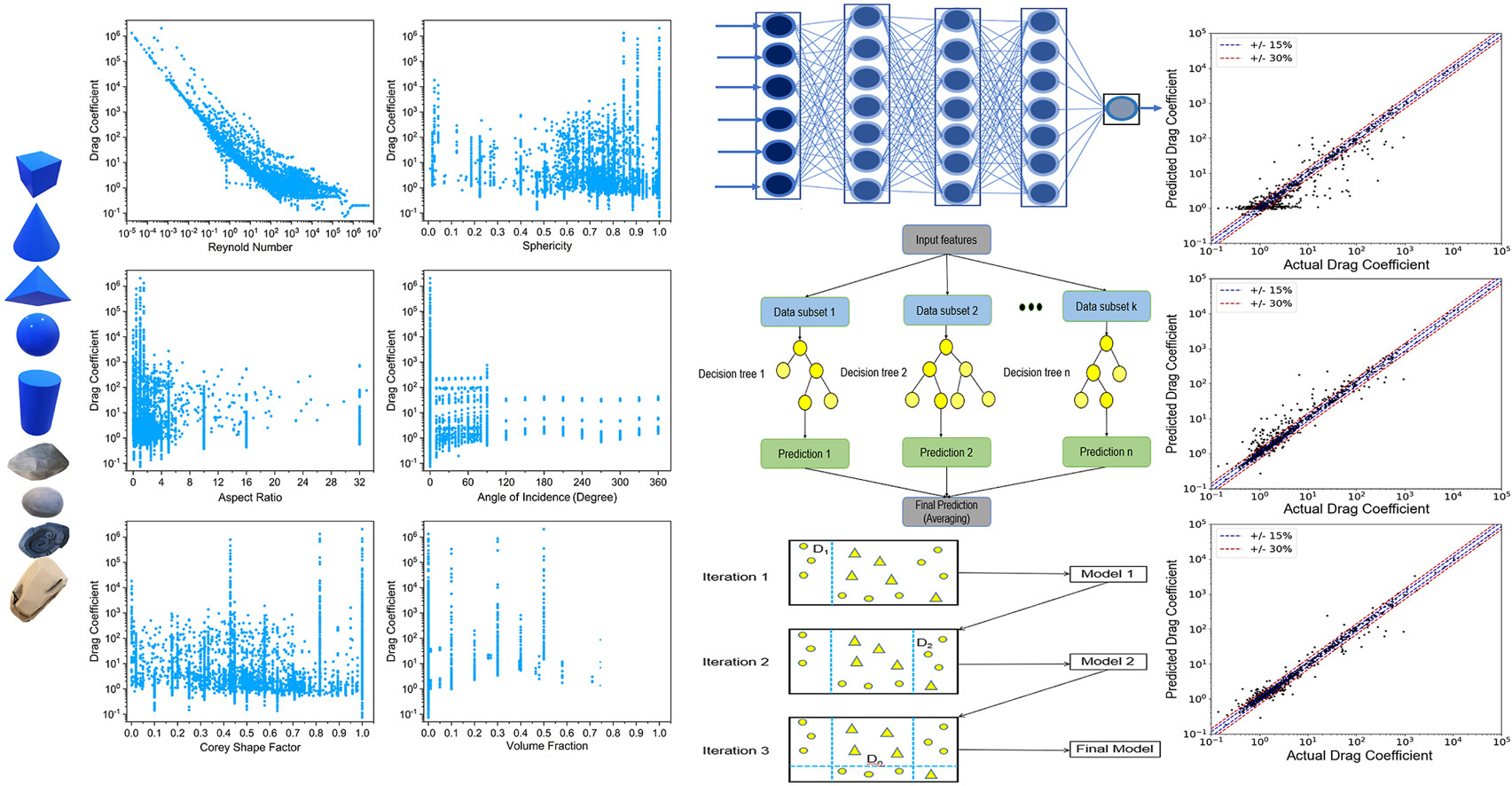
• Database of 5000 points with six input features created.

• Three machine learning models were developed to predict drag coefficient.

• AdaBoost outperformed Neural Networks and Random Forest.

• Drag coefficient is highly sensitive to variations in Reynolds number and volume fraction.

Abstract

Non-spherical particles are extensively encountered in the process industry such as feedstock or catalysts e.g., energy, food, pharmaceuticals, and chemicals. The design of equipment used to process these particles is highly dependent upon the accurate and reliable modeling of hydrodynamics of particulate media involved. Drag coefficient of these particles is the most significant of all parameters. A universal model to predict the drag coefficient of such particles has not yet been developed due to the diversity and complexity of particle shapes and sizes. Taking this into consideration, we propose a unique approach to model the drag coefficient of non-spherical particles using machine learning (ML) to move towards generalization. A comprehensive database of approximately five thousand data points from reliable experiments and high-resolution simulations was compiled, covering a wide range of conditions. The drag coefficient was modeled as a function of Reynolds number, sphericity, Corey Shape Factor, aspect ratio, volume fraction, and angle of incidence. Three ML techniques—Artificial Neural Networks, Random Forest, and AdaBoost—were used to train the models. All models demonstrated strong generalization when tested on unseen data. However, AdaBoost outperformed the others with the lowest MAPE (20.1%) and MRD (0.069). Additional analysis on excluded data confirmed the robust predictive abilities and generalization of the proposed model. The models were also evaluated across three flow regimes—Stokes, transitional, and turbulent—to further assess their generalization. A comparative analysis with well-known empirical correlations, such as Haider and Levenspiel and Chien, showed that all ML models outperformed traditional approaches, with AdaBoost achieving the best results. The current work demonstrates that new generated ML techniques can be reliably used to predict drag coefficient of non-spherical particles paving way towards generalization of ML approach.

Graphical abstract

Keywords

Drag coefficient; Non-spherical; Neural network; Random forest; AdaBoost

文章导读