
Gaussian integral method for void fraction
Alireza Kianimoqadam, Justin Lapp*
Keywords: Void fraction; Discrete element method; Fluid-Particle interaction; CFD-DEM; Gaussian integral method
DOI: 10.1016/j.partic.2025.10.014
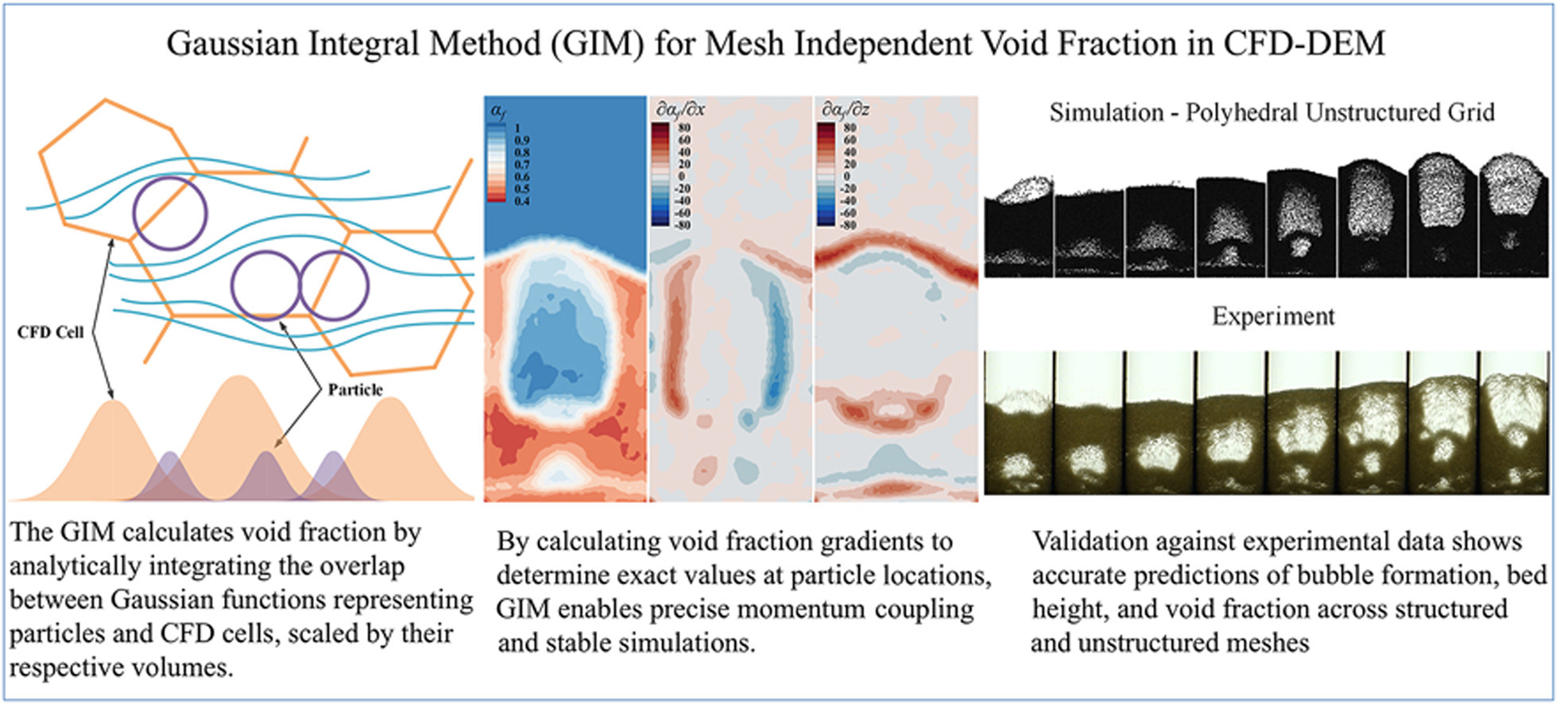
本研究提出了一种高斯积分法(Gaussian Integral Method, GIM),用于颗粒流体系统CFD-DEM模拟中精确计算空隙率。该方法基于高斯核平滑技术,在Sun & Xiao(International Journal of Multiphase Flow, 2015)提出的扩散方法基础上构建,通过解析计算粒子与网格单元本身的缩放高斯函数重叠,直接获得网格内粒子的体积分数,从而彻底摆脱传统扩散类方法对瞬态扩散方程求解和伪时间步迭代的依赖,显著降低了计算开销。该方法解决了精确计算孔隙率的难题,尤其适用于涉及复杂几何结构和多种网格类型的模拟。
主要结论:
1. GIM是一种适用于多种网格(包括结构化与非结构化多面体网格)的通用方法,无需像其他高斯方法那样进行特殊边界处理,增强了该方法在含有复杂几何结构的工业仿真中的适用性。
2. 通过优化,使GIM方法摆脱了对网格分辨率和网格类型的依赖。基于颗粒和网格体积调整高斯函数标准偏差,该方法能在较大的颗粒-网格体积比范围内适用。
3. 利用Wachem等的实验数据对GIM方法进行了验证,表明在CFD-DEM模拟中采用GIM方法可获得符合实际的流化床动力学结果。该方法准确再现了相对压力波动、气泡形成及床层高度变化,与实验观测结果高度吻合。
4. 采用GIM的多面体网格相较于等效分辨率的结构化网格表现更优,所得结果与实验数据吻合度更高,这归功于多面体网格邻近单元数量更多,从而实现了更精确的流体场梯度计算。
5. GIM方法能够精确计算空隙率梯度,这对于在DEM求解器中准确估算颗粒周围的局部空隙率至关重要。该精度的提升,有助于更好地模拟颗粒-流体的相互作用,从而获得更可靠的模拟结果。
总之,GIM方法兼具多功能性、高精度及无需特殊边界处理的特性,使其成为提升各类工业应用中多相流模拟精度的有力工具。未来研究可通过为粒子与单元分别设定标准差对方法实施进一步优化,或将其应用扩展至更复杂的多相系统。
相关研究成果发表于PARTICUOLOGY(Volume 108),欢迎感兴趣的读者扫描下方二维码或者点击文末“阅读原文”进入ScienceDirect官网阅读、下载!

供稿:原文作者
排版:《颗粒学报》编辑部
文章信息
Kianimoqadam, A., & Lapp, J. (2026). Gaussian integral method for void fraction. Particuology, 108, 125-142. https://doi.org/10.1016/j.partic.2025.10.014
